There are 5 distinct parametrisations of the FitzHugh-Nagumo model implemented in this package. They are explained in turn below
This is the most commonly encountered parametrisation of the FitzHugh-Nagumo model. The target, two dimensional process (Y,X) solves the following stochastic differential equation:
\[\begin{align*}
d Y_t &= \frac{1}{\epsilon}\left( Y_t - Y_t^3-X_t + s \right )dt,\\
dX_t &= \left( \gamma Y_t - X_t + \beta \right )dt + \sigma dW_t.
\end{align*}\]
The proposal is taken to be a guided proposal with auxiliary law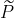 
induced by the linear diffusion obtained by linearising FitzHugh-Nagumo diffusion at an end-point:
\[\begin{align*}
d \widetilde{Y}_t &= \frac{1}{\epsilon}\left( \left( 1-3y_T^2 \right )\widetilde{Y}_t - \widetilde{X}_t + s + 2y_T^3 \right)dt,\\
d\widetilde{X}_t &= \left( \gamma \widetilde{Y}_t - \widetilde{X}_t + \beta \right)dt + \sigma dW_t.
\end{align*}\]
The target stochastic differential equations is re-parametrised in such a way that the first coordinate is given by the integrated second coordinate:
\[\begin{align*}
d Y_t &= \dot{Y}_t dt,\\
d\dot{Y}_t &= \frac{1}{\epsilon}\left( (1-\gamma)Y_t -Y_t^3 -\epsilon \dot{Y}_t + s - \beta + \left( 1-3Y_t^2 \right)\dot{Y}_t \right)dt + \frac{\sigma}{\epsilon}dW_t.
\end{align*}\]
The auxiliary law 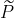is now induced by a pair: (I,B), where B is a scaled Brownian motion and I is an integrated B:
\[\begin{align*}
d I_t &= B_tdt,\\
dB_t &= \frac{\sigma}{\epsilon}dW_t.
\end{align*}\]
The stochastic differential equation solved by the target process is the same as in :simpleAlter. However, the auxliary law 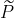is induced by a two-dimensional diffusion, where the second coordinate is a linear diffusion obtained from linearising 
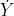at an end-point and the first coordinate is an integrated second coordinate. If only the first coordinate is observed the proposal takes a form:
\[\begin{align*}
d\widetilde{Y}_t &= \widetilde{X}_t dt,\\
d\widetilde{X}_t &= \frac{1}{\epsilon}\left[ \left( 1-\gamma-3y_T^2 \right )\widetilde{Y}_t +\left( 1-\epsilon-3y_T^2 \right )\widetilde{X}_t + \left(2y_T^3+s-\beta \right )\right ]dt + \frac{\sigma}{\epsilon}dW_t.
\end{align*}\]
On the other hand, if both coordinates are observed, the proposal is given by:
\[\begin{align*}
d\widetilde{Y}_t &= \widetilde{X}_t dt,\\
d\widetilde{X}_t &= \frac{1}{\epsilon}\left[ \left( 1-\gamma-3y_T^2 - 6y_T\dot{y}_T \right )\widetilde{Y}_t +\left( 1-\epsilon -3y_T^2 \right )\widetilde{X}_t + \left(2y_T^3+s-\beta + 6y_T^2\dot{y}_T \right )\right ]dt + \frac{\sigma}{\epsilon}dW_t.
\end{align*}\]
It is defined analogously to :simpleAlter, the only difference being that an additional step is taken of redefining the parameters:
\[s\leftarrow \frac{s}{\epsilon},\quad \beta\leftarrow\frac{\beta}{\epsilon},\quad \sigma\leftarrow\frac{\sigma}{\epsilon},\quad \gamma\leftarrow\frac{\gamma}{\epsilon},\quad \epsilon\leftarrow\frac{1}{\epsilon}.\]
This results in the target law of the form:
\[\begin{align*}
d Y_t &= \dot{Y}_t dt,\\
d\dot{Y}_t &= \left( (\epsilon-\gamma)Y_t -\epsilon Y_t^3 -\dot{Y}_t + s - \beta + \epsilon\left( 1-3Y_t^2 \right)\dot{Y}_t \right)dt + \sigma dW_t.
\end{align*}\]
And the proposal law:
\[\begin{align*}
d I_t &= B_tdt,\\
dB_t &= \sigma dW_t.
\end{align*}\]
It is defined analogously to :complexAlter, the only difference being that an additional step is taken of redefining the parameters (just as it was done in :simpleConjug above). Consequently the target law is as given above, in the section on :simpleConjug parametrisation, whereas proposal law is given by:
\[\begin{align*}
d\widetilde{Y}_t &= \widetilde{X}_t dt,\\
d\widetilde{X}_t &= \left\{ \left[ \epsilon\left(1-3y_T^2 - 6y_T\dot{y}_T \right )-\gamma \right ]\widetilde{Y}_t +\left[ \epsilon\left( 1-3y_T^2 \right)-1 \right ]\widetilde{X}_t + \left[\epsilon\left(2y_T^3+ 6y_T^2\dot{y}_T \right ) +s-\beta \right]\right \}dt + \sigma dW_t.
\end{align*}\]